1 📑Metadata

The Transformer architecture has become a dominant choice in many domains, such as natural language processing and computer vision. Yet, it has not achieved competitive performance on popular leaderboards of graph-level prediction compared to mainstream GNN variants. Therefore, it remains a mystery how Transformers could perform well for graph representation learning. In this paper, we solve this mystery by presenting Graphormer, which is built upon the standard Transformer architecture, and could attain excellent results on a broad range of graph representation learning tasks, especially on the recent OGB Large-Scale Challenge. Our key insight to utilizing Transformer in the graph is the necessity of effectively encoding the structural information of a graph into the model. To this end, we propose several simple yet effective structural encoding methods to help Graphormer better model graph-structured data. Besides, we mathematically characterize the expressive power of Graphormer and exhibit that with our ways of encoding the structural information of graphs, many popular GNN variants could be covered as the special cases of Graphormer.

2 💡Note

2.1 论文试图解决什么问题？

Whether Transformer architecture is suitable to model graphs ?
How Transformers can perform well for graph representation learning ?

2.2 这是否是一个新的问题？

No, this issue of leveraging Transformers into the graph domain has been explored before.

2.3 这篇文章要验证一个什么科学假设？

With novel graph structural encodings, Graphormer has strong expressiveness as many popular GNN variants are just its special cases.

2.4 有哪些相关研究？如何归类？谁是这一课题在领域内值得关注的研究员？

2.4.1 Preliminary

2.4.1.1 Graph Neural Network (GNN)

Typically, modern GNNs follow a learning schema that iteratively updates the representation of a node by aggregating representations of its first or higher-order neighbors. 1. AGGREGATE: to gather the information from neighbors. 2. COMBINE: to fuse the information from neighbors into the node representation. 3. For graph representation tasks: . - READOUT: to aggregate node features of the final iteration into the representation of the entire graph.

2.4.1.2 Transformer

Each Transformer layer has two parts: a self-attention module and a position-wise feed-forward network (FFN). 1. Input: 2. The input is projected by three matrices and to the corresponding representations , , . 3. Self-attention:

2.4.2.1 Graph Transformer

Pure Transformer architectures (stacked by transformer layers) with modifications on graph representation tasks 1. Additional GNN employed in attention sub-layer to produce vectors of Q, K, and V 2. Long-range residual connection. 3. FFN to produce node and edge representations. 4. Use Laplacian eigenvector as positional encodings 5. The attention mechanism in Transformers on graph data should only aggregate the information from neighborhood to ensure graph sparsity.
6….

2.4.2.2 Structural Encodings in GNNs

Path and Distance in GNNs.
1. Path-based attention:
  1. To calculate the attention probabilities.
  2. To model the influence between the center node and its higher-order neighbors.
2. Distance-weighted aggregation scheme on graph:
  1. Position-aware graph neural networks.
3. Distance encoding:
  1. One-hot feature of the distance as extra node attribute.
Positional Encoding in Transformer on Graph.
1. To help the model capture the node position information.
2. Examples:
  1. Graph-BERT: an absolute WL-PE, an intimacy based PE and a hop based PE
  2. Absolute Laplacian PE
Edge Feature.
1. Attention: The edge feature is weighted by the similarity of the features of its two nodes.
2. GIN
3. Project edge features to an embedding vector.

2.5 🔴论文中提到的解决方案之关键是什么？

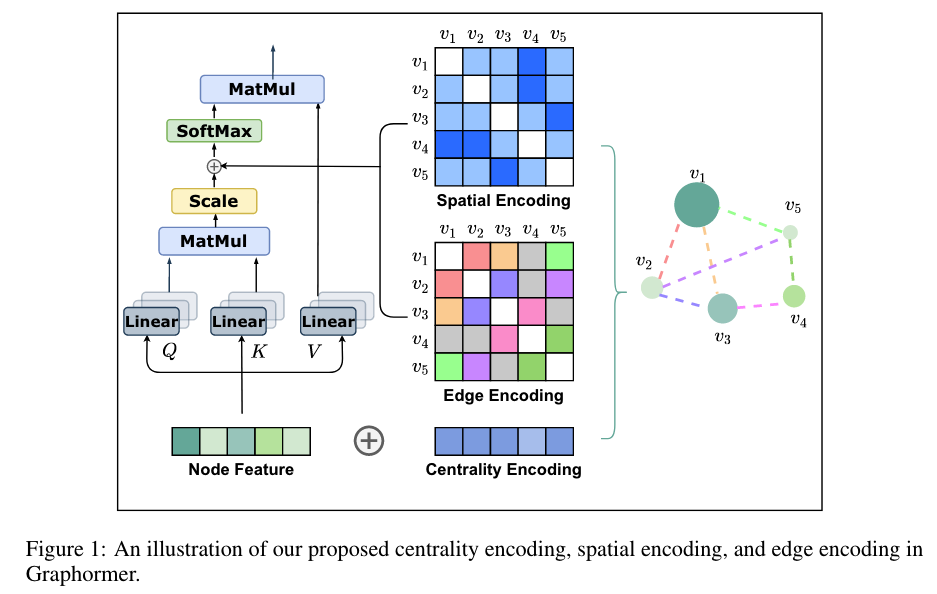
2.5.1 Structural Encodings in Graphormer

To leverage the structural information of graphs into the Transformer model.

Centrality Encoding（Node importance）
1. Assign each node two real-valued embedding vectors according to its indegree and outdegree
2. Add it to the node features as the input:
  - are learnable embedding vectors
  - For undirected graphs, and could be unified to .
Spatial Encoding (Structural information of a graph)
1. Transformer need explicit absolute or relative positional encodings for its global receptive field. But for graphs, nodes are not arrange as an ordered sequence.
2. SPD can Be Used to Improve WL-Test
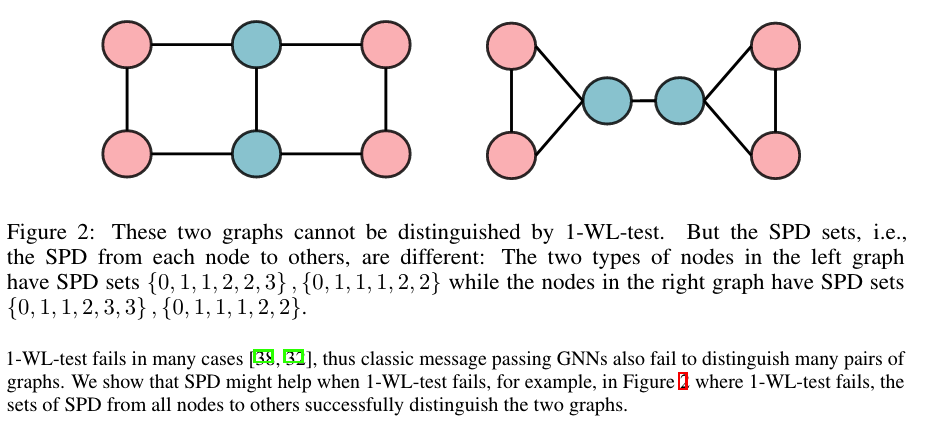
3. For any graph , consider a function which measures the spatial relation between and in graph
  1. The function can be defined by the connectivity between the nodes in the graph.
  2. The distance of the shortest path (SPD) between and if the two nodes are connected. If not, we set the output of to be a special value, i.e., -1.
  3. Assign each (feasible) output value a learnable scalar which will serve as a bias term in the self-attention module.
Edge Encoding in the Attention
1. In many graph tasks, edges also have structural features.
  1. Edge features are added to the associated nodes' features.
  2. For each node, its associated edges' features will be used together with the node features in the aggregation.
2. Previous ways of using edge feature cannot leverage edge information in representation of the whole graph.
3. Find (one of) the shortest path from to , and compute an average of the dot-products of the edge feature and a learnable embedding along the path.

2.5.2 Implementation Details of Graphormer

Graphormer Layer
Special Node
1. Add a special node called [VNode] to the graph.
2. Make connection between [VNode] and each node individually.
3. The representation of [VNode] has been updated as normal nodes in graph.
4. The representation of the entire graph would be the node feature of [VNode] in the final layer.

2.5.3 How Powerful is Graphormer?

Do these modifications make Graphormer more powerful than other GNN variants?

By choosing proper weights and distance function , the Graphormer layer can represent AGGREGATE and COMBINE steps of popular GNN models such as GIN, GCN, GraphSAGE.
1. MEAN AGGREGATE
  1. Setting if and otherwise where is the SPD.
  2. Setting and to be the identity matrix.
2. SUM AGGREGATE
  - First perform MEAN aggregation and then multiply the node degrees.
3. MAX AGGREGATE
  1. Setting if and otherwise where is the SPD.
  2. Setting which is the -th standard basis; and the bias term of to be ; and , where is the temperature that can be chosen to be large enough so that the softmax function can approximate hard max and is the vector whose elements are all 1.
4. COMBINE
  1. Setting if and otherwise where is the SPD.
  2. Setting and to be the identity matrix.
  3. The FFN module can approximate any COMBINE function by the universal approximation theorem of FFN.
By choosing proper weights, every node representation of the output of a Graphormer layer without additional encodings can represent MEAN READOUT functions.
1. Setting
2. Setting the bias terms of to be , and to be the identity matrix where should be much larger than the scale of
3. dominates the Spatial Encoding term.

2.6 这篇论文到底有什么贡献？

This paper explored the direct application of Transformers to graph representation.

2.7 下一步呢？有什么工作可以继续深入？

The quadratic complexity of the self-attention module restricts Graphormer's application on large graphs.
Performance improvement could be expected by leveraging domain knowledge-powered encodings on particular graph datasets.
An applicable graph sampling strategy is desired for node representation extraction with Graphormer.